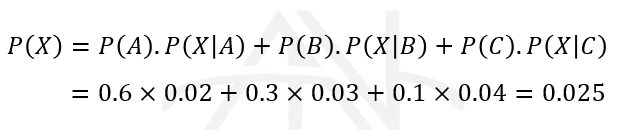قضیه بیز چیست؟ #
قضیه بیز (Bayes’ Theorem) بیان می کند که احتمال یک فرضیه خاص هم از اطلاعات فعلی (داده ها) و هم از دانش قبلی به دست می آید. اطلاعات پیشین ممکن است نتیجه تجارب یا آزمایشات قبلی، یا حتی حدس های آموخته شده از تجربه باشد. با وجودی که قرن هاست از رویکرد بیزی استفاده می شود، آمار بیزی همچنان کاربرد دارد و فایده آن را در کاربردهای بسیاری نشان داده شده است، به طوریکه برخی اعتقاد دارند، هیچ دانشمند داده ای نمی تواند بدون درک کامل احتمال شرطی و استنتاج بیزی کار کند.
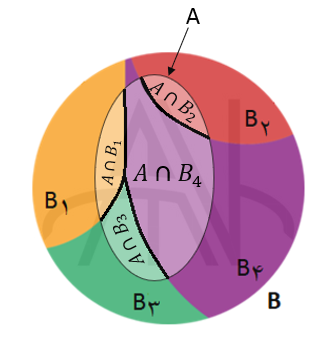
اگر مجموعه همه وقایع ممکن را Ω (امگا) یا فضای نمونه بنامیم و A یک عضو از فضای نمونه باشد، احتمال فضای نمونه P(Ω) = 1 است و احتمال پیشامد یا رخداد A را با P(A)نشان می دهیم که برابر است با:
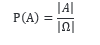
که در آن |A| برابر تعداد اعضای پیشامد A یا اندازه بزرگی پیشامد A می باشد. اگر |A| برابر با |Ω| باشد، احتمال A یعنی P(A) حداکثر برابر با ۱ است.
اگر B رخداد دیگری در فضای نمونه باشد، احتمال پیشامد آن مشابه A محاسبه می شود. همچنین، فضای مشترک دو رخداد A و B یا به عبارتی رخداد هم زمان این دو (اشتراک) با A∩B یا به طور ساده با AB نشان داده می شود. احتمال پیشامد A به شرط B یا همان احتمال شرطی به صورت زیر تعریف می شود :
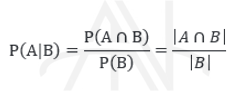
احتمال شرطی احتمال وقوع پیشامدی است که در آینده رخ می دهد و بر اساس نتایج قبلی پیشامدها محاسبه می شود.
از رابطه بالا می توان نتیجه گرفت:
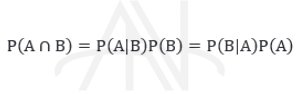
و بالاخره قضیه بیز عبارت است از:
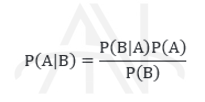
در قضیه بیز به P(A|B) احتمال پسین (Posterior Probability) ، به P(A) احتمال پیشین (Perior Probability) و به P(B|A) درست نمایی (Likelihood) و به P(B) احتمال حاشیه ای (Marginal Probability) می گوییم.
قضیه بیز طیف وسیعی از کاربردها دارد، به ویژه در زمینه هایی که با به روز رسانی احتمالات بر اساس داده های جدید سروکار دارند. با قضیه بیز می توان احتمال پسین یا به روز (updated) را با استفاده از احتمال شرطی پیشامدها محاسبه کرد. بنابراین قضیه بیز زمانی قابل اجرا است که احتمال شرطی یک پیشامد داده شود که از آن برای یافتن احتمال معکوس پیشامد استفاده می شود.
قضیه بیز تعمیم یافته #
فرض کنید مجموعه {B۱,B۲,⋯,Bn } یک افراز از فضای نمونه باشد. اگر C پیشامد دلخواهی از فضای نمونه باشد و،P(C)≠۰ آنگاه به ازای k=1,2,…,n داریم:
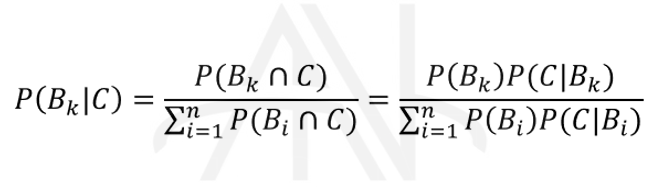
همچنین می توان رابطه زیر را نیز از قضیه بیز به دست آورد:
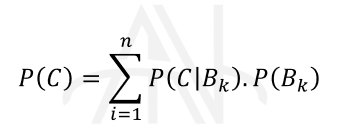
آن پیشامد از افراز یک مجموعه
مثال ۱ #
سه ظرف کاملا مشابه با محتویات زیر مفروض هستند. ظرفی را به تصادفی انتخاب کرده و مهره ای از آن خارج می کنیم. اگر این مهره سفید باشد، مطلوب است احتمال اینکه ظرف اول را انتخاب کرده باشیم.
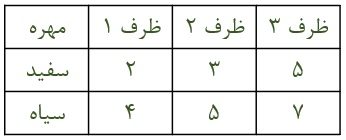
در نظر میگیریم:
- – Bi: پیشامد اینکه ظرف i ام را انتخاب کنیم و i=1, 2, 3
- – C: پیشامد اینکه مهره سفید باشد
ابتدا با استفاده از جدول بالا، معلومات مسئله را می نویسیم:
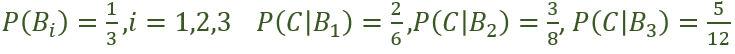
با استفاده از قضیه بیز، احتمال شرطی انتخاب مهره از ظرف اول به شرط اینکه بدانیم مهره سفید است یعنی P(B۱|C) را به دست می آوریم:
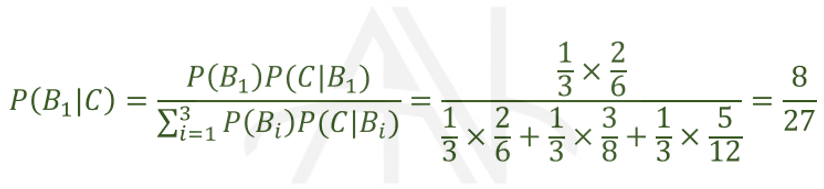
مثال ۲ #
سه ماشین A و B و C به ترتیب ۶۰%، ۳۰% و ۱۰% کل محصولات کارخانه ای را تولید می کنند. درصد محصولات معیوب این ماشینها به ترتیب برابر ۲%، ۳% و ۴% است. از میان محصولات این کارخانه محصولی را به صورت تصادفی انتخاب می کنیم، احتمال اینکه محصولی که انتخاب کرده ایم معیوب باشد، چقدر است؟
در نظر میگیریم:
- – A , B , C: پیشامد اینکه محصولات ماشینهایی با همین نام را انتخاب کنیم
- – X: پیشامد اینکه محصول انتخاب شده معیوب باشد
با استفاده از صورت مسئله، معلومات را مینویسیم:
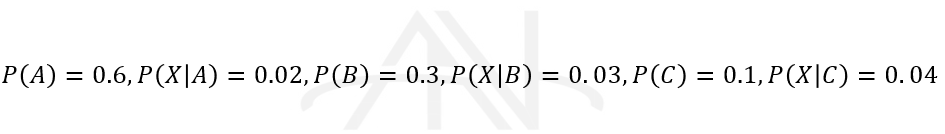
مطلوب است محاسبه P(X) که با توجه به داشتن احتمال شرطی X به تمامی افرازها (A,Bو C) با استفاده از قضیه بیز به دست می آوریم: