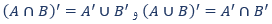نظریه مجموعه ها

نظریه مجموعه ها (Set Theory) شاخه ای از منطق ریاضی است که مجموعه ها را مطالعه می کند.

مجموعه #

عبارت است از یک دسته از اشیاء که کاملا مشخص باشند و بتوان گفت هر شیء مفروض، متعلق به مجموعه هست یا نیست. مجموعه را با حروف بزرگ A، B و … نشان می‌دهند.

توجه: یک مجموعه با اعضای خود مشخص می شود، پس اگر دسته اشیاء کاملا مشخص نباشند، آن را مجموعه نمی گوییم. مثلا « افراد خوشبخت» ، «مردان شیک پوش» چون مبهم هستند، قابلیت تعریف به عنوان مجموعه را ندارند.

عضو مجموعه #

هر یک از اشیای مجموعه را عضو مجموعه می‌نامیم  و به صورت xϵB نشان می دهیم. اگر x عضو B  نباشد، آن را به صورت x∉B نشان می دهیم.

طرز نشان دادن مجموعه ها #

الف- نمایش مجموعه به وسیله نام بردن اعضاء: #

اگر مجموعه متناهی باشد (یعنی تعداد اعضای آن قابل شمارش باشد)، عضوها را داخل دو ابرو {} قرارداده و با یک کاما «،» از هم جدا می کنیم. مثال: مجموعه اعداد فرد کمتر از ۱۰ :  

A={1,3,5,7,9}

ب- نمایش مجموعه به وسیله نمودار وِن: #

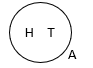
با استفاده از نمودار ون (Venn) اعضای مجموعه را داخل یک چندضلعی یا درون یک دایره نشان میدهیم. . مثال: مجموعه نتایج حاصل از پرتاب یک سکه را به صورت زیر نشان می دهیم که درآن شیر یا H و خط یا T اعضای مجموعه نتیجه پرتاب یک سکه هستند.

پ- نمایش مجموعه به وسیله علائم ریاضی: #

مجموعه را با بیان خاصیتی معین مشخص می کنیم: مثال: اگر C مجموعه شهرهای ایران باشد: 

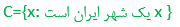
مجموعه تُهی #

اگر مجموعه دارای هیچ عضوی نباشد آن را تهی یا مجموعه خالی می نامیم و آن را با نماد {}یا ∅ نشان میدهیم. مثال:

مجموعه های جدا #

دو مجموعه غیرتهی که هیچ عضو مشترکی نداشته باشند را دو مجموعه جدا از هم می گوییم.

زیرمجموعه #

اگر هر عضو B، عضوی از A باشد، مجموعه B را زیرمجموعه مجموعه A میگوییم و مینویسیم B⊆A ، به عبارت دیگر:

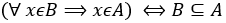
با نمودار ون به صورت زیر نشان می دهیم:

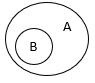
اگر حداقل یک عضو B‌، عضوی از A نباشد آنگاه میگوییم B زیرمجموعه A نیست و به صورت B⊄A یا B⊈A نشان می دهیم.

مجموعه مرجع #

هر مجموعه را می توان زیرمجموعه ای از یک مجموعه ثابت در نظر گرفت که به آن مجموعه مرجع گفته می شود و آن را با U‌ نشان می دهند. در نمایش ون، مجموعه مرجع را به صورت یک مستطیل و مجموعه های موردنظر را درون مستطیل رسم می کنیم.

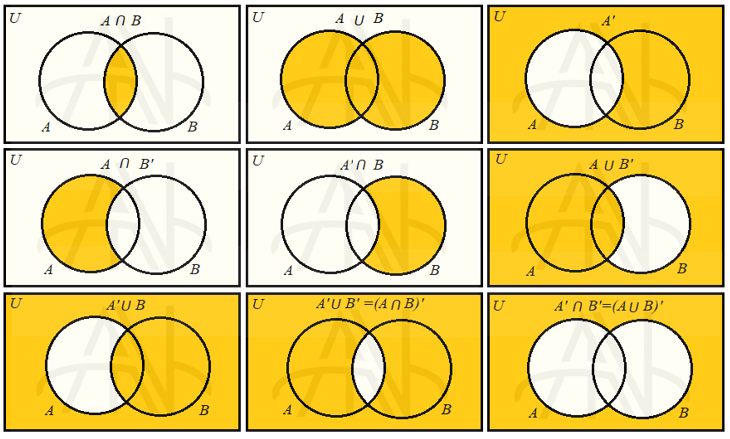
مثلا اگر A و B‌ دو زیرمجموعه ‌از مجموعه مرجع U باشند:

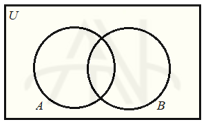
مجموعه متمم #

اگر A‌ زیرمجموعه ای دلخواه از یک مجموعه مرجع U‌ باشد، متمم مجموعه A‌ که با A’‌ نشان داده می شود، مجموعه تمام عضوهای U‌ است که در A نیست. به عبارت دیگر:

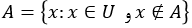
توجه کنید که A‌ و A’ دو مجموعه جدا از هم هستند.

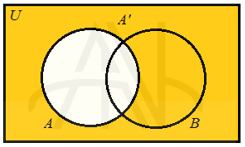
مثال: اگر  A={1,2,5,8} و U={1,2,3,4,5,6,7,8,9,10} آنگاه متمم A‌ برابر است با:  A ́={۳,۴,۶,۷,۹,۱۰} 

اجتماع دو مجموعه #

#

اجتماع دو مجموعه A‌ و B مجموعه ای است که شامل تمام عضوهای متعلق به مجموعه های A‌ و B‌ یا هر دو آنها باشد. اجتماع دو مجموعه را به صورت A∪B نشان می دهیم :

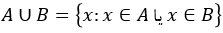
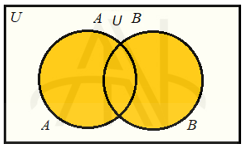
مثال:  A={1,2,5,8} و B={2,3,5,10} 

A∪B={1,2,3,5,8,10}

اشتراک دو مجموعه #

اشتراک دو مجموعه A‌ و B مجموعه ای است که شامل تمام عضوهای مشترک متعلق به مجموعه های A‌ و B‌ باشد. اشتراک دو مجموعه را به صورت A∩B نشان می دهیم:

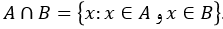
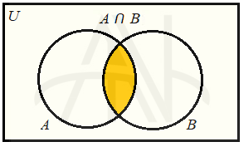
مثال:  A={1,2,5,8} و B={2,3,5,10} 

A∩B={2,5}

تفاضل دو مجموعه #

تفاضل دو مجموعه A‌ و B را با نماد A-B نشان میدهیم و مجموعه عضوهایی از A‌ است که در B نیست.

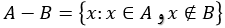
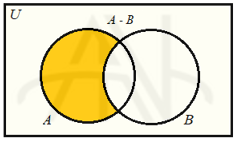
مثال:  A={1,2,5,8} و B={2,3,5,10}

A-B={1,8} و B-A={3,10}

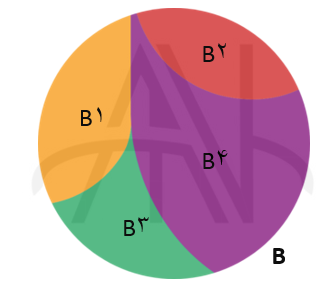
افراز مجموعه #

افراز یک مجموعه (Partition of a set) یعنی تبدیل کردن آن به زیرمجموعه‌هایش به طوری که، اشتراک هر کدام از آن زیرمجموعه‌ها با یکدیگر مجموعه تهی باشد (مجموعه‌های مجزا) و اجتماع تمامی زیر مجموعه‌ها برابر با مجموعه افراز شده باشد.

خواص مجموعه ها #

اگر A , B, C‌ سه مجموعه باشند آنگاه خواص زیر برقرار است:

الف- خاصیت جابجایی:

A∪B=B∪A و A∩B=B∩A

ب- خاصیت شرکت پذیری:

A∩(B∩C)=(A∩B)∩C و A∪(B∪C)=(A∪B)∪C

پ- خاصیت توزیع پذیری:

A∪(B∩C)=(A∪B)∩C و A∩(B∪C)=(A∩B)∪C

ت- قانون دمورگان: