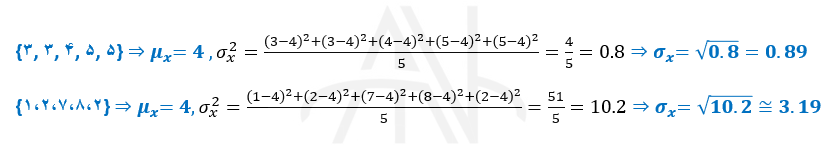پارامترهای مرکزی مانند میانگین در همه موارد جوابگوی نیاز تصمیم گیرنده نیستند. به عنوان مثال ممکن است دو جامعه آماری متفاوت، میانگین یکسان داشته باشند. بنابراین توزیعهای آماری را با استفاده از یک یا چند پارامتر پراکندگی (Dispersion Parameter) از نظر شدت نوسان داده ها حول مرکزشان مورد بررسی و مقایسه قرارمی دهند و معروفترین آنها عبارتند از واریانس، انحراف معیار، دامنه تغییرات.
توجه داشته باشید پراکندگی زمانی مفهوم پیدا می کند که هر یک از داده ها نسبت به یک مبدا (مرکز) مقایسه شوند. بهترین مرکز برای داده ها میانگین است زیرا دارای خواص جبری است و می توان اعمال ریاضی و جبری روی آن اعمال کرد.
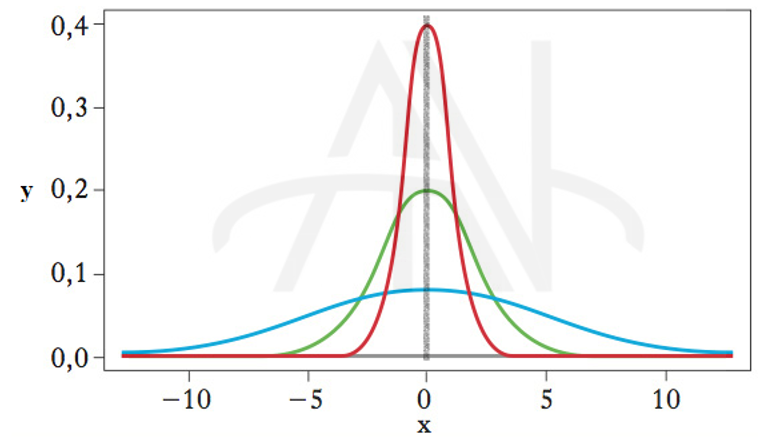
همانطور که در شکل بالا مشاهده می شود، هر سه جامعه آماری که با رنگهای متفاوت نشان داده شده اند، میانگین یکسان برابر صفر دارند ولی داده های جامعه آماری قرمزرنگ ، حول میانگین (عدد ۰) متمرکزتر از بقیه هستند و جامعه آماری آبی رنگ پراکنده تر از بقیه حول میانگین هستند.
دامنه تغییرات #
دامنه تغییرات (Variation Range) از تفاضل کوچکترین مشاهده از بزرگترین مشاهده حساب می شود و هر چه دامنه تغییرات بزرگتر باشد یعنی داده ها پراکندگی بیشتری دارند.
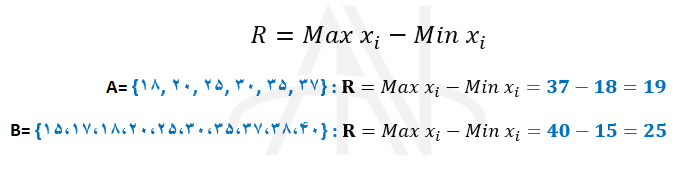
همانطور که در مثال بالا مشاهده می شود، بر اساس پارامتر پراکندگی دامنه تغییرات، جامعه آماری A پراکندگی کمتری نسبت به جامعه آماری B دارد.
واریانس #
واریانس یا وردایی (Variance) مقدار متوسط مربع اختلاف مقادیر و مشاهدات جامعه از میانگین است. آن را با σx۲ نشان می دهند و از یکی از دو رابطه زیر حساب می شود :
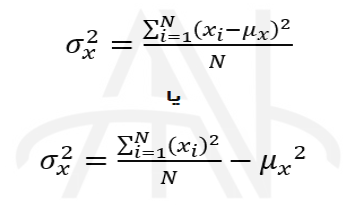
که در آن μx میانگین جامعه ، N تعداد کل مشاهدات،xi مشاهده iام است.
با نماد سیگما (∑) آشنا نیستند؟ به این صفحه بروید.
مثال #
به شیوه محاسبه واریانس در دو مثال زیر توجه کنید:
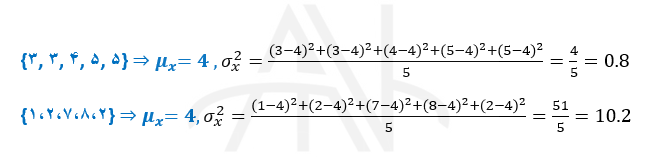
توجه: چون واریانس به صورت مجذور (توان دو) است، تفسیر آن ساده نیست. مثلا اگر محاسبه میزان پراکندگی درآمد جامعه مدنظر باشد، واحد واریانس ریال به توان دو است که اعلام پراکندگی به صورت ملموس نیست. بنابراین بیشتر از جذر (ریشه دوم) واریانس استفاده می کنند و به آن شاخص انحراف معیار می گویند.
انحراف معیار #
انحراف معیار (Standard Deviation)، جذر (ریشه دوم) واریانس است که واحد آن با واحد اصلی متغیر یکسان است و آن را با σx نشان می دهند
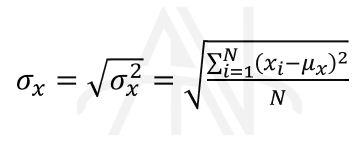
مثال #
در شکل زیر دو مثال از محاسبه انحراف معیار مشاهده می شود: