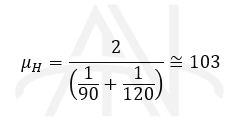پارامتر مرکزی، هر معیار عددی است که معرف مرکز مجموعه داده ها باشد و مقدار آن، تعیین کننده نماینده ای است که مشاهدات، اطراف آن توزیع شده اند. میانه، مُد و میانگین از مهمترین پارامترهای مرکزی می باشند.
میانه #
میانه (Median)، نقطه/مقدار میانی در مجموعه مرتب شده داده هاست.
در محاسبه میانه حتما باید مجموعه داده را از کوچک به بزرگ مرتب کنیم.
الف- محاسبه میانه وقتی تعداد نقاط داده فرد باشد #
اگر تعداد داده ها فرد باشد، میانه برابر با عدد وسطی است.
مثال: برای محاسبه میانه پنج عدد ۲۰, ۱۷, ۱۲, ۳۳ , ۴۲ ابتدا اعداد را از کوچک به بزرگ مرتب می کنیم:
۱۲,۱۷,۲۰,۳۳,۴۲
مشاهده می شود عدد وسطی (سومی در بین ۵ عدد) میانه است. و معمولا به صورت زیر می نویسیم:
Md=۲۰
ب- محاسبه میانه وقتی تعداد نقاط داده زوج باشد #
اگر تعداد داده ها زوج باشد، میانه برابر با میانگین حسابی دو عدد وسطی است.
مثال: برای محاسبه میانه چهار عدد ۲۰, ۱۷, ۱۲, ۳۳ ابتدا اعداد را از کوچک به بزرگ مرتب می کنیم:
۱۲,۱۷,۲۰,۳۳
و میانگین حسابی دو عدد وسطی را محاسبه می کنیم:
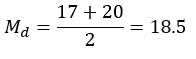
مُد یا نما #
مُد یا نما (Mode)، عضو (یا اعضایی) از جامعه است که بیشترین تکرار را در میان اعضاء یا مشاهدات داشته باشد.
- مثال ۱: در مجموعه اعداد 2 و۲و ۳ و ۵و ۳و ۲ مشاهده می شود که عدد ۲ بیشترین تکرار را دارد. پس مد در این مجموعه برابر عدد ۲ است و آن را به این صورت می نویسیم: Mo=۲
- مثال ۲: در مجموعه اعداد ۳ و ۳و ۴ و ۵ و ۶ و ۶ مشاهده می شود که هر دو عدد ۳ و ۶ به طور مساوی بیشترین تکرار را دارند. پس مد این مجموعه برابر ۳ و ۶ است : ۶ و Mo=۲.
- مثال ۳: در مجموعه اعداد ۱ و ۲ و ۳ و ۴ و ۵ مشاهده می شود که همه اعداد به یک اندازه (یک بار) تکرار شده اند. پس این مجموعه مُد ندارد یا فاقد مُد است و می نویسیم: Mo=φ. که در آن φ را فی می خوانیم که علامت مجموعه تُهی یا پوچ است.
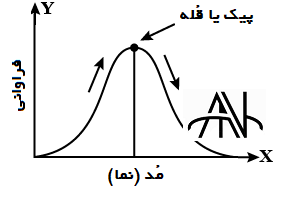
در شکل فوق مشاهده می شود که مد یا نما در نقاط داده (محور X) در نقطه ای قرار داد که پیک یا قله نمودار یا به عبارت دیگر بیشترین تکرار(فراوانی) درمجموعه داده را دارد.
میانگین #
میانگین (Average) اصلی ترین و پرکاربردترین پارامتر مرکزی است. اگر داده ها روی یک محور منظم ردیف شوند، مقدار میانگین دقیقا در نقطه تعادل یا مرکز ثقل توزیع قرار میگیرد. با توجه به صفت مورد اندازه گیری، میانگین انواعی دارد که عبارتند از: میانگین حسابی، میانگین حسابی موزون، میانگین پیراسته، میانگین وینزوری، میانگین هندسی، میانگین هارمونیک، …
میانگین حسابی #
میانگین حسابی (Arithmetic Mean) ساده که معمولا مترادف با میانگین درنظر گرفته می شود، با استفاده از رابطه زیر به دست می آید:

با نماد سیگما (∑) آشنا نیستند؟ به این صفحه بروید.
مثال #
نمرات ۱۰ دانشجوی کلاس به شرح جدول زیر می باشد. مطلوب است محاسبه میانگین حسابی نمرات:

میانگین موزون یا وزن دار #
میانگین موزون یا وزن دار(Weighted Mean)، هنگامی استفاده می شود که مشاهدات وزنهای متفاوت دارند (مانند میانگین نمرات دروس با ضرایب (وزن) مختلف). میانگین حسابی موزون با استفاده از رابطه زیر به دست می آید:

با نماد سیگما (∑) آشنا نیستند؟ به این صفحه بروید.
مثال #
نمرات ۱۰ دانشجوی کلاس به شرح زیر است:
۲۰، ۱۹، ۱۸، ۱۶، ۱۴، ۱۷،۱۸، ۱۷، ۲۰، ۱۵
ابتدا جدول فراوانی مشاهدات را به دست آورده و سپس میانگین حسابی موزون را محاسبه می کنیم:
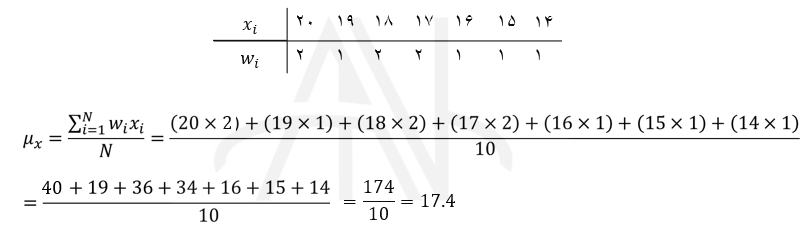
میانگین پیراسته #
میانگین پیراسته (Trimmed Mean)، زمانی استفاده می شود که حتی تعداد معدودی از مشاهدات با بقیه همخوانی نداشته باشند (خیلی بزرگ یا خیلی کوچک باشند). زیرا اعداد خیلی بزرگ یا کوچک در میانگین جامعه اثر گذار هستند.
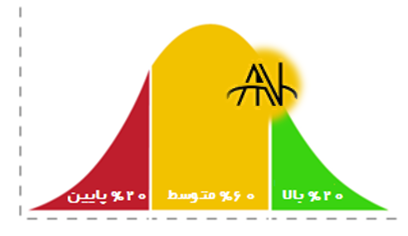
در این حالت، یک حد برای پیرایش مشاهدات تعیین می شود که آن را معمولا با LN نشان می دهیم. مثلا اگر LN=25% باشد، یعنی ۲۵% بالا و پایین مشاهدات مرتب شده را ابتدا حذف کرده و سپس از بقیه مشاهدات میانگین حسابی می گیریم.
نکته: برای محاسبه میانگین پیراسته ابتدا مشاهدات را از کوچک به بزرگ مرتب می کنیم.
مثال #
میانگین پیراسته اعداد زیر با LN=20% را به دست آورید:

توجه کنید که چون تعداد مشاهدات برابر ۱۰ است، بنابراین ۲۰% مشاهدات برابر عدد ۲ خواهد بود. بنابراین دو تا از بالا و دو تا از پایین مشاهدات مرتب شده را حذف می کنیم. حال میانگین حسابی بقیه مشاهدات را محاسبه می کنیم:
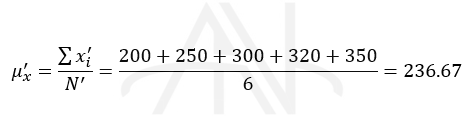
توجه: در عمل ممکن است برای محاسبه میانگین پیراسته به جای روش بالا از حد یا کران بالا و پایین مشاهدات استفاده شود. مثلا اعداد بزرگتر از LN1 یا کوچکتر از LN2 را حذف کنیم. محاسبه این کران هم از مسائل تحلیل داده است و بسته به موضوع و مشاهدات، روشهای مختلف دارد.
میانگین وینزوری #
میانگین وینزوری (Winsorized Mean)، نوعی میانگین پیراسته است که به جای حذف مشاهدات کوچکتر یا بزرگتر، مقدار عددی LN کوچکتر یا بزرگتر را قرار می دهند.
مثال #
در مثال بالا، بجای حذف دو عدد کوچک ۱۱۰ و ۱۰۰، مشاهده کوچک بعدی از لیست یعنی عدد ۲۰۰ و بجای حذف دو عدد بزرگ ۱۰۰۰و ۲۰۰۰، مشاهده بزرگ بعدی از لیست یعنی عدد ۳۵۰ را جایگزین کرده و در محاسبه میانگین نهایی اعداد جایگزین شده را لحاظ می کنیم:
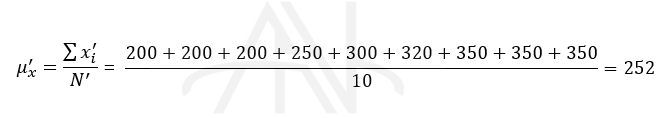
میانگین هندسی #
میانگین هندسی (Geometric Mean) برای محاسبه میانگین اندازه های نسبی مانند نسبتها، درصدها، نرخهای رشد و شاخصها استفاده می شود. میانگین هندسی N مشاهده (عدد)، برابر است با ریشه Nام حاصلضرب آن اعداد.
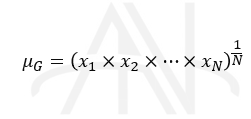
مثلا برای محاسبه میانگین نرخ سود یک شرکت، متوسط درصد کارایی کارکنان و … از میانگین هندسی استفاده می کنیم.
میانگین هارمونیک #
میانگین هارمونیک (Harmonic Mean)، هنگامی استفاده می شود که مشاهدات، مقیاس ترکیبی داشته باشند، مثل کیلومتر در ساعت، دور در ثانیه، نفر ساعت، ….و برابر است با عکس میانگین حسابی معکوس آن اندازه ها
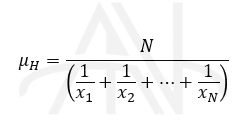
مثال #
راننده ای مسافت تهران قم را با سرعت ۹۰ کیلومتر در ساعت و مسیر برگشت را با سرعت ۱۲۰ کیلومتر در ساعت می رود. متوسط سرعت راننده را حساب کنید: